linear regression hw 3

作业内容：

Linear Models with R (2nd Edition)第2章所有题

Exercise 1

The dataset teengamb concerns a study of teenage gambling in Britain. Fit a regression model with the expenditure on gambling as the response and the sex, status, income and verbal score as predictors. Present the output.

rm(list=ls())

pkgs <- c('tidyverse','faraway','skimr','ggplot2')
invisible(lapply(pkgs, function(x) suppressMessages(library(x,character.only = TRUE))))

data(teengamb)
glimpse(teengamb)

Rows: 47
Columns: 5
$ sex    <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, …
$ status <int> 51, 28, 37, 28, 65, 61, 28, 27, 43, 18, 18, 43, 30, 28, 38, 38,…
$ income <dbl> 2.00, 2.50, 2.00, 7.00, 2.00, 3.47, 5.50, 6.42, 2.00, 6.00, 3.0…
$ verbal <int> 8, 8, 6, 4, 8, 6, 7, 5, 6, 7, 6, 6, 4, 6, 6, 8, 8, 5, 8, 9, 8, …
$ gamble <dbl> 0.00, 0.00, 0.00, 7.30, 19.60, 0.10, 1.45, 6.60, 1.70, 0.10, 0.…

(a) What percentage of variation in the response is explained by these predictors?

model <- lm(gamble ~ ., data = teengamb )
modelsum <- summary(model)
modelsum$r.squared

[1] 0.5267234

(b) Which observation has the largest (positive) residual? Give the case number.

num <- unname(which.max(modelsum$residuals))
num

[1] 24

(c) Compute the mean and median of the residuals.

mean(modelsum$residuals)

[1] 2.645638e-16

median(modelsum$residuals)

[1] -1.451392

(d) Compute the correlation of the residuals with the fitted values.

plot(modelsum$residuals,predict(model))

cor(modelsum$residuals,predict(model))

[1] -1.030987e-16

(e) Compute the correlation of the residuals with the income.

cor(modelsum$residuals,teengamb$income)

[1] -2.006086e-17

(f) For all other predictors held constant, what would be the difference in predicted expenditure on gambling for a male compared to a female?

summary(model)$coefficients['sex','Estimate']

[1] -22.11833

Exercise 2

The dataset uswages is drawn as a sample from the Current Population Survey in 1988. Fit a model with weekly wages as the response and years of education and experience as predictors. Report and give a simple interpretation to the regression coefficient for years of education. Now fit the same model but with logged weekly wages. Give an interpretation to the regression coefficient for years of education. Which interpretation is more natural?

data('uswages')
glimpse(uswages)

Rows: 2,000
Columns: 10
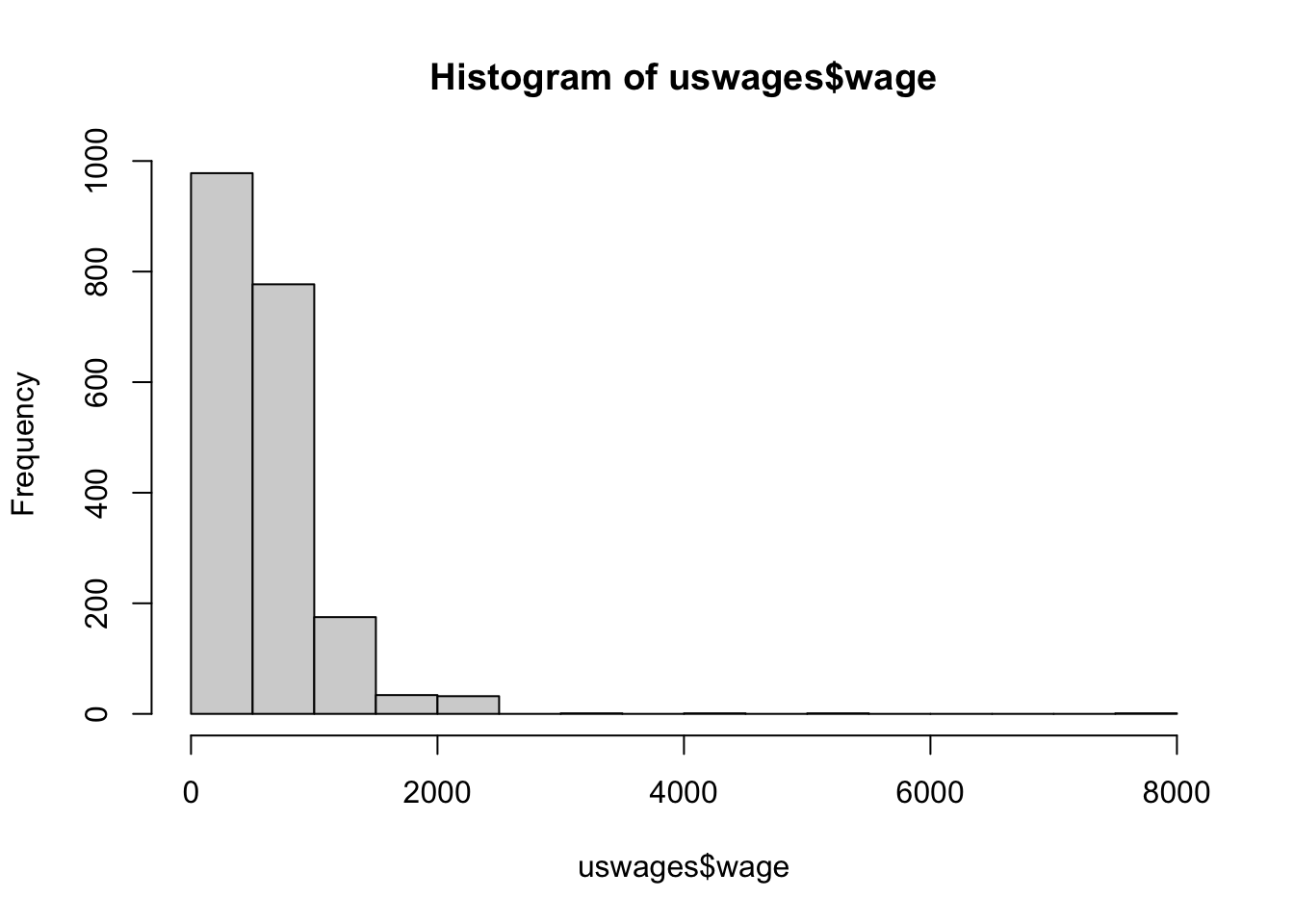
$ wage  <dbl> 771.60, 617.28, 957.83, 617.28, 902.18, 299.15, 541.31, 148.39, …
$ educ  <int> 18, 15, 16, 12, 14, 12, 16, 16, 12, 12, 9, 14, 17, 14, 14, 10, 1…
$ exper <int> 18, 20, 9, 24, 12, 33, 42, 0, 36, 37, 20, 29, 16, 21, 11, 10, 8,…
$ race  <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ smsa  <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1…
$ ne    <int> 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0…
$ mw    <int> 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0…
$ so    <int> 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1…
$ we    <int> 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0…
$ pt    <int> 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0…

hist(uswages$wage)

# GGally::ggpairs(uswages[,c(1:3)])
model <- lm(wage ~ educ + exper, uswages)
summary(model)$coefficients['educ','Estimate']

[1] 51.17527

model <- lm(log(wage) ~ educ + exper, uswages)
#summary(model)$coefficients['educ','Estimate']
exp(summary(model)$coefficients['educ','Estimate'])

[1] 1.094728

Y偏态分布，应该log转换后在拟合模型，注意log转化后要转化回来再解释，此外该模型的R-squard很小，模型意义不大

Exercise 3

In this question, we investigate the relative merits of methods for computing the coefficients. Generate some artificial data by:

> x <- 1:20 
> y <- x+rnorm(20)

Fit a polynomial in x for predicting y. Compute \(\bar \beta\) in two ways — by lm() and by using the direct calculation described in the chapter. At what degree of polynomial does the direct calculation method fail? (Note the need for the I() function in fitting the polynomial, that is, lm(y ~ x + I(x^2))

# lm()法
x <- 1:20
y <- x + rnorm(20)
m <- lm(y ~ x + I(x^2))
summary(m)

Call:
lm(formula = y ~ x + I(x^2))

Residuals:
    Min      1Q  Median      3Q     Max 
-2.1225 -0.5200 -0.2275  0.6088  1.7176 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.731908   0.738251  -0.991    0.335    
x            1.184552   0.161910   7.316 1.21e-06 ***
I(x^2)      -0.006675   0.007489  -0.891    0.385    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9923 on 17 degrees of freedom
Multiple R-squared:  0.9775,    Adjusted R-squared:  0.9748 
F-statistic: 368.7 on 2 and 17 DF,  p-value: 9.979e-15

# 直接计算法
x <- model.matrix(~ x + I(x^2))
solve(crossprod(x,x), crossprod(x, y))

                    [,1]
(Intercept) -0.731907764
x            1.184552428
I(x^2)      -0.006675383

# 循环
# 计算函数

f <- function(z){
x <- 1:20
y <- x + rnorm(20)
x <- model.matrix(~ x + I(x^z))
solve(crossprod(x,x), crossprod(x, y))
}

 #map(2:10,function(z) f(z))

Exercise 4

The dataset prostate comes from a study on 97 men with prostate cancer who were due to receive a radical prostatectomy. Fit a model with lpsa as the response and lcavol as the predictor. Record the residual standard error and the R2. Now add lweight, svi, lbph, age, lcp, pgg45 and gleason to the model one at a time. For each model record the residual standard error and the R2. Plot the trends in these two statistics.

data("prostate")

model <- lm(lpsa ~ lcavol, prostate)
# residual standard error
summary(model)$sigma

[1] 0.7874994

# R2
summary(model)$r.squared

[1] 0.5394319

add_variable <- c("lcavol","lweight", "svi", "lbph", "age", "lcp", "pgg45", "gleason")

results <- data.frame(sigma=NULL,r2=NULL,formula=NULL)
for(i in 1:length(add_variable)){
  
if (i == 1) {
    model_formula <- paste("lpsa ~", add_variable[i])
  } else {
    model_formula <- paste(model_formula, "+", add_variable[i])
  }

  summodel <- summary(lm(formula(model_formula), data = prostate))

  result <- data.frame(sigma=summodel$sigma,r2=summodel$r.squared,formula=model_formula)
  results <- rbind(results,result)
}
print(results)

      sigma        r2
1 0.7874994 0.5394319
2 0.7506469 0.5859345
3 0.7168094 0.6264403
4 0.7108232 0.6366035
5 0.7073054 0.6441024
6 0.7102135 0.6451130
7 0.7047533 0.6544317
8 0.7084155 0.6547541
                                                             formula
1                                                      lpsa ~ lcavol
2                                            lpsa ~ lcavol + lweight
3                                      lpsa ~ lcavol + lweight + svi
4                               lpsa ~ lcavol + lweight + svi + lbph
5                         lpsa ~ lcavol + lweight + svi + lbph + age
6                   lpsa ~ lcavol + lweight + svi + lbph + age + lcp
7           lpsa ~ lcavol + lweight + svi + lbph + age + lcp + pgg45
8 lpsa ~ lcavol + lweight + svi + lbph + age + lcp + pgg45 + gleason

# Create a plot for sigma
plot(1:8, results$sigma, type = 'l', col = 'blue', lwd = 2,
     ylim = c(0.6, 0.9),  # Set the y-axis limits here
     xlab = 'Model Number', ylab = 'Value',
     main = 'Residual Standard Error and R-squared')

points(1:8, results$sigma, col = 'blue', pch = 19)

r2_normalized <- results$r2 * (max(results$sigma) / max(results$r2))

lines(1:8, r2_normalized, col = 'red', lwd = 2)

points(1:8, r2_normalized, col = 'red', pch = 19)

legend('topright', legend = c('Residual Standard Error', 'R-squared (scaled)'),
       col = c('blue', 'red'), lty = 1, pch = 19)

Exercise 5

Using the prostate data, plot lpsa against lcavol. Fit the regressions of lpsa on lcavol and lcavol on lpsa. Display both regression lines on the plot. At what point do the two lines intersect?

model1 <- lm(lcavol ~ lpsa, prostate)
model2 <- lm(lpsa ~ lcavol, prostate)

# -0.50858+0.74992*(1.50730+0.71932*x)=x
# -0.50858+0.74992*1.50730+0.74992*0.71932*x=x
x <- (-0.50858+0.74992*1.50730)/(1-0.74992*0.71932)
y <- 1.50730+0.71932*x

ggplot(prostate, aes(lcavol, lpsa)) +
  geom_point(alpha = .5) +
  geom_line(aes(x = predict(model1), color = "lcavol ~ lpsa")) +
  geom_line(aes(y = predict(model2), color = "lpsa ~ lcavol")) +
  geom_point(aes(y =y, x = x), shape = 1, size = 5)

Warning in geom_point(aes(y = y, x = x), shape = 1, size = 5): All aesthetics have length 1, but the data has 97 rows.
ℹ Please consider using `annotate()` or provide this layer with data containing
  a single row.

Exercise 6

Thirty samples of cheddar cheese were analyzed for their content of acetic acid, hydrogen sulfide and lactic acid. Each sample was tasted and scored by a panel of judges and the average taste score produced. Use the cheddar data to answer the following:

(a) Fit a regression model with taste as the response and the three chemical contents as predictors. Report the values of the regression coefficients.

data("cheddar")
model <- lm(taste ~ ., cheddar)
sumary(model)

             Estimate Std. Error t value Pr(>|t|)
(Intercept) -28.87677   19.73542 -1.4632 0.155399
Acetic        0.32774    4.45976  0.0735 0.941980
H2S           3.91184    1.24843  3.1334 0.004247
Lactic       19.67054    8.62905  2.2796 0.031079

n = 30, p = 4, Residual SE = 10.13071, R-Squared = 0.65

(b) Compute the correlation between the fitted values and the response. Square it. Identify where this value appears in the regression output.

cor(model$fitted.values, cheddar$taste)^2

[1] 0.6517747

(c) Fit the same regression model but without an intercept term. What is the value of R2 reported in the output? Compute a more reasonable measure of the goodness of fit for this example.

model <- lm(taste ~ -1+., cheddar)
summary(model)$r.squared

[1] 0.8877059

#cor(model$fitted.values, cheddar$taste)^2

(d) Compute the regression coefficients from the original fit using the QR decomposition showing your R code.

model <- lm(taste ~ ., cheddar)
m_mat <- model.matrix(model)

qr_decomp <- qr(m_mat)

backsolve(
  qr.R(qr_decomp), # upper-right
  t(qr.Q(qr_decomp)) %*% cheddar$taste
)

            [,1]
[1,] -28.8767696
[2,]   0.3277413
[3,]   3.9118411
[4,]  19.6705434

Exercise 7

An experiment was conducted to determine the effect of four factors on the resistivity of a semiconductor wafer. The data is found in wafer where each of the four factors is coded as − or + depending on whether the low or the high setting for that factor was used. Fit the linear model resist ∼ x1 + x2 + x3 + x4.

1. Extract the X matrix using the model.matrix function. Examine this to determine how the low and high levels have been coded in the model.

data("wafer")
glimpse(wafer)

Rows: 16
Columns: 5
$ x1     <fct> -, +, -, +, -, +, -, +, -, +, -, +, -, +, -, +
$ x2     <fct> -, -, +, +, -, -, +, +, -, -, +, +, -, -, +, +
$ x3     <fct> -, -, -, -, +, +, +, +, -, -, -, -, +, +, +, +
$ x4     <fct> -, -, -, -, -, -, -, -, +, +, +, +, +, +, +, +
$ resist <dbl> 193.4, 247.6, 168.2, 205.0, 303.4, 339.9, 226.3, 208.3, 220.0, …

model <- lm(resist ~ ., wafer)
x <- model.matrix(model)
x

   (Intercept) x1+ x2+ x3+ x4+
1            1   0   0   0   0
2            1   1   0   0   0
3            1   0   1   0   0
4            1   1   1   0   0
5            1   0   0   1   0
6            1   1   0   1   0
7            1   0   1   1   0
8            1   1   1   1   0
9            1   0   0   0   1
10           1   1   0   0   1
11           1   0   1   0   1
12           1   1   1   0   1
13           1   0   0   1   1
14           1   1   0   1   1
15           1   0   1   1   1
16           1   1   1   1   1
attr(,"assign")
[1] 0 1 2 3 4
attr(,"contrasts")
attr(,"contrasts")$x1
[1] "contr.treatment"

attr(,"contrasts")$x2
[1] "contr.treatment"

attr(,"contrasts")$x3
[1] "contr.treatment"

attr(,"contrasts")$x4
[1] "contr.treatment"

2. Compute the correlation in the X matrix. Why are there some missing values in the matrix?

cor(x)

Warning in cor(x): the standard deviation is zero

            (Intercept) x1+ x2+ x3+ x4+
(Intercept)           1  NA  NA  NA  NA
x1+                  NA   1   0   0   0
x2+                  NA   0   1   0   0
x3+                  NA   0   0   1   0
x4+                  NA   0   0   0   1

因为截距项全部为1，且其余变量都是01编码

3. What difference in resistance is expected when moving from the low to the high level of x1?

sumary(model)

            Estimate Std. Error t value  Pr(>|t|)
(Intercept)  236.781     14.769 16.0322 5.645e-09
x1+           25.762     13.210  1.9502 0.0770849
x2+          -69.888     13.210 -5.2906 0.0002561
x3+           43.587     13.210  3.2996 0.0070828
x4+          -14.488     13.210 -1.0967 0.2961929

n = 16, p = 5, Residual SE = 26.41970, R-Squared = 0.8

4. Refit the model without x4 and examine the regression coefficients and standard errors? What stayed the the same as the original fit and what changed?

model2 <- lm(resist ~ x1+x2+x3, wafer)
sumary(model2)

            Estimate Std. Error t value  Pr(>|t|)
(Intercept)  229.538     13.321 17.2312 7.883e-10
x1+           25.762     13.321  1.9340 0.0770472
x2+          -69.888     13.321 -5.2464 0.0002056
x3+           43.587     13.321  3.2721 0.0066773

n = 16, p = 4, Residual SE = 26.64201, R-Squared = 0.78

# x <-  model.matrix(model2)
# cor(x)

5. Explain how the change in the regression coefficients is related to the correlation matrix of X.

x <- model.matrix(model2) # 就是截距项的原因
solve(t(x) %*% x) #奇异矩阵，也就是矩阵不可逆 行或列是线性相关的，也就是矩阵的行列式为 0

            (Intercept)    x1+    x2+    x3+
(Intercept)       0.250 -0.125 -0.125 -0.125
x1+              -0.125  0.250  0.000  0.000
x2+              -0.125  0.000  0.250  0.000
x3+              -0.125  0.000  0.000  0.250

# x <- model.matrix(model2)[,-1] # 就是截距项的原因
# solve(t(x) %*% x)

Exercise 8

An experiment was conducted to examine factors that might affect the height of leaf springs in the suspension of trucks. The data may be found in truck. The five factors in the experiment are set to − and + but it will be more convenient for us to use −1 and +1. This can be achieved for the first factor by:

truck$B <- sapply(truck$B, function(x) ifelse(x=="-",-1,1))

Repeat for the other four factors.

1. Fit a linear model for the height in terms of the five factors. Report on the value of the regression coefficients.

data("truck")
glimpse(truck)

Rows: 48
Columns: 6
$ B      <fct> -, +, -, +, -, +, -, +, -, +, -, +, -, +, -, +, -, +, -, +, -, …
$ C      <fct> -, -, +, +, -, -, +, +, -, -, +, +, -, -, +, +, -, -, +, +, -, …
$ D      <fct> -, -, -, -, +, +, +, +, -, -, -, -, +, +, +, +, -, -, -, -, +, …
$ E      <fct> -, +, +, -, +, -, -, +, -, +, +, -, +, -, -, +, -, +, +, -, +, …
$ O      <fct> -, -, -, -, -, -, -, -, +, +, +, +, +, +, +, +, -, -, -, -, -, …
$ height <dbl> 7.78, 8.15, 7.50, 7.59, 7.94, 7.69, 7.56, 7.56, 7.50, 7.88, 7.5…

truck <- truck %>% mutate_if(is.factor, ~ ifelse(. == "-", -1, 1))
model <- lm(height ~ ., truck)
sumary(model)

             Estimate Std. Error  t value  Pr(>|t|)
(Intercept)  7.636042   0.022909 333.3160 < 2.2e-16
B            0.110625   0.022909   4.8288 1.852e-05
C           -0.088125   0.022909  -3.8467 0.0004005
D           -0.014375   0.022909  -0.6275 0.5337453
E            0.051875   0.022909   2.2644 0.0287751
O           -0.129792   0.022909  -5.6655 1.201e-06

n = 48, p = 6, Residual SE = 0.15872, R-Squared = 0.64

2. Fit a linear model using just factors B, C, D and E and report the coefficients. How do these compare to the previous question? Show how we could have anticipated this result by examining the X matrix.

model2 <- update(model, . ~ . -O)
sumary(model2)

             Estimate Std. Error  t value  Pr(>|t|)
(Intercept)  7.636042   0.030073 253.9154 < 2.2e-16
B            0.110625   0.030073   3.6785 0.0006483
C           -0.088125   0.030073  -2.9304 0.0054015
D           -0.014375   0.030073  -0.4780 0.6350709
E            0.051875   0.030073   1.7250 0.0917167

n = 48, p = 5, Residual SE = 0.20835, R-Squared = 0.37

cor(model.matrix(model2 )) 

Warning in cor(model.matrix(model2)): the standard deviation is zero

            (Intercept)  B  C  D  E
(Intercept)           1 NA NA NA NA
B                    NA  1  0  0  0
C                    NA  0  1  0  0
D                    NA  0  0  1  0
E                    NA  0  0  0  1

自变量间无相关性，系数没变

3. Construct a new predictor called A which is set to B+C+D+E. Fit a linear model with the predictors A, B, C, D, E and O. Do coefficients for all six predictors appear in the regression summary? Explain.

truck$A <- rowSums(truck[, c("B", "C", "D", "O")])

model3 <- update(model, . ~ . + A)
sumary(model3)

Coefficients: (1 not defined because of singularities)
             Estimate Std. Error  t value  Pr(>|t|)
(Intercept)  7.636042   0.022909 333.3160 < 2.2e-16
B            0.110625   0.022909   4.8288 1.852e-05
C           -0.088125   0.022909  -3.8467 0.0004005
D           -0.014375   0.022909  -0.6275 0.5337453
E            0.051875   0.022909   2.2644 0.0287751
O           -0.129792   0.022909  -5.6655 1.201e-06

n = 48, p = 6, Residual SE = 0.15872, R-Squared = 0.64

4. Extract the model matrix X from the previous model. Attempt to compute \(\bar \beta\) from (XT X)−1XT y. What went wrong and why?

x <- model.matrix(model3)
solve(t(x) %*% x)

x <- model.matrix(model3)[,-7] #还是因为奇异性 因为A 不对
solve(t(x) %*% x)

            (Intercept)          B          C          D          E          O
(Intercept)  0.02083333 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
B            0.00000000 0.02083333 0.00000000 0.00000000 0.00000000 0.00000000
C            0.00000000 0.00000000 0.02083333 0.00000000 0.00000000 0.00000000
D            0.00000000 0.00000000 0.00000000 0.02083333 0.00000000 0.00000000
E            0.00000000 0.00000000 0.00000000 0.00000000 0.02083333 0.00000000
O            0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.02083333

5. Use the QR decomposition method as seen in Section 2.7 to compute \(\bar \beta\). Are the results satisfactory?

qr_decomp <- qr(model.matrix(model3))
backsolve(
  qr.R(qr_decomp), # upper-right
  t(qr.Q(qr_decomp)) %*% truck$height
)

              [,1]
[1,]  7.636042e+00
[2,]  1.870143e+13
[3,]  1.870143e+13
[4,]  1.870143e+13
[5,]  5.715314e-02
[6,]  1.870143e+13
[7,] -1.870143e+13

6. Use the function qr.coef to correctly compute \(\bar \beta\) .

#qr.coef 来计算回归系数  是一种有效且稳定的方法，特别是在处理可能存在多重共线性的问题时
qr.coef(qr_decomp, truck$height)

(Intercept)           B           C           D           E           O 
  7.6360417   0.1106250  -0.0881250  -0.0143750   0.0518750  -0.1297917 
          A 
         NA